

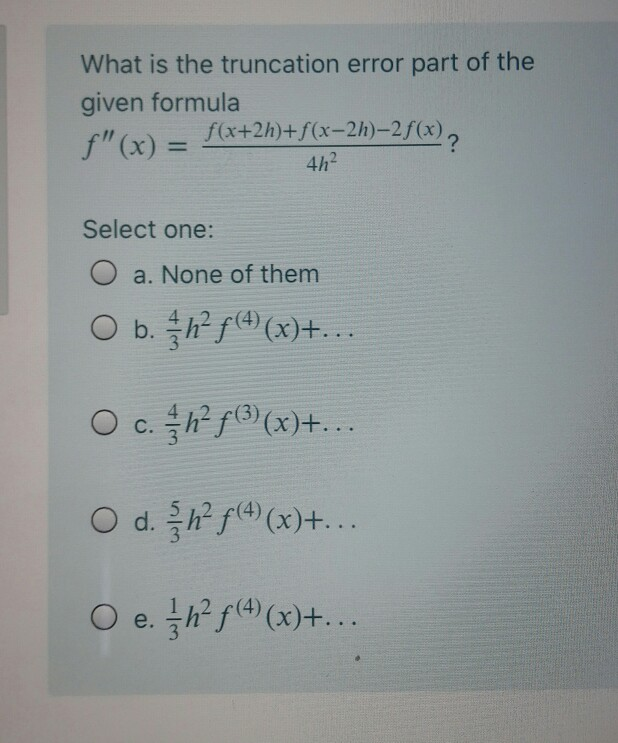
Assume that the polynomial has the desired traits but IS NOT the Taylor polynomial. I'm new to this forum so I dunno know how to make the math symbols all purty-like so I'll just type things out in English. Hello, I think I may have found a way to prove it (I also have it for homework :D).
Does anyone have any suggestions or jumping off points for this proof? I'm positive that I'm over-complicating the problem, but I just cannot figure out where to start. However, perhaps because I keep thinking about how to prove the converse, I'm completely stuck on how to go from knowing that Q and K exist to make the initial inequality true, to proving that Q is the Taylor polynomial. \left|f(x) - Q(x)\right| \leq K\left|x - a\right|^, since this would just be proving the Lagrange error bound theorem, and would just involve some integration/induction. I'm given that the function f(x) is n times differentiable over an interval I and that there exists a polynomial Q(x) of degree less than or equal to n s.t.


 0 kommentar(er)
0 kommentar(er)
